Чи існує «сінгапурська математика» та навіщо вона українським дітям?

Диво-методики, які допоможуть кожній дитині опанувати алгебру та геометрію, дуже цікавлять батьків і вчителів. Завідувачка відділу математичної та інформатичної освіти Інституту педагогіки НАПН України, кандидатка педагогічних наук, експертка ГС «Освіторія» Дарина Васильєва працювала над адаптацією сінгапурських матеріалів для українських шкіл. Тому поділилася нюансами під час вебінару «Особливості сінгапурської методики математики» на базі тренінгового центру ГС «Освіторія». Занотували для вас головні секрети «сінгапурської математики».

Диво почалося з освіти

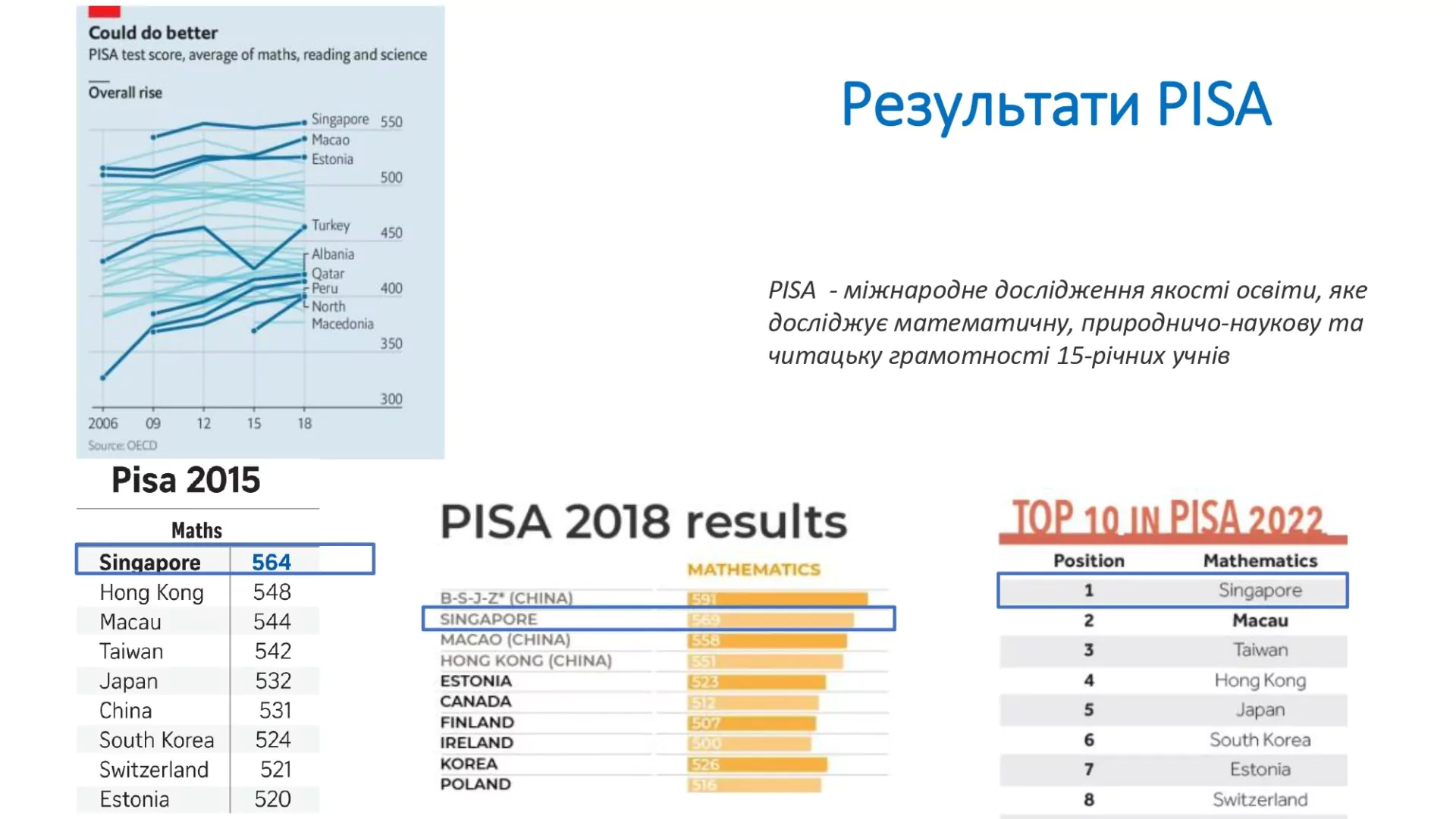
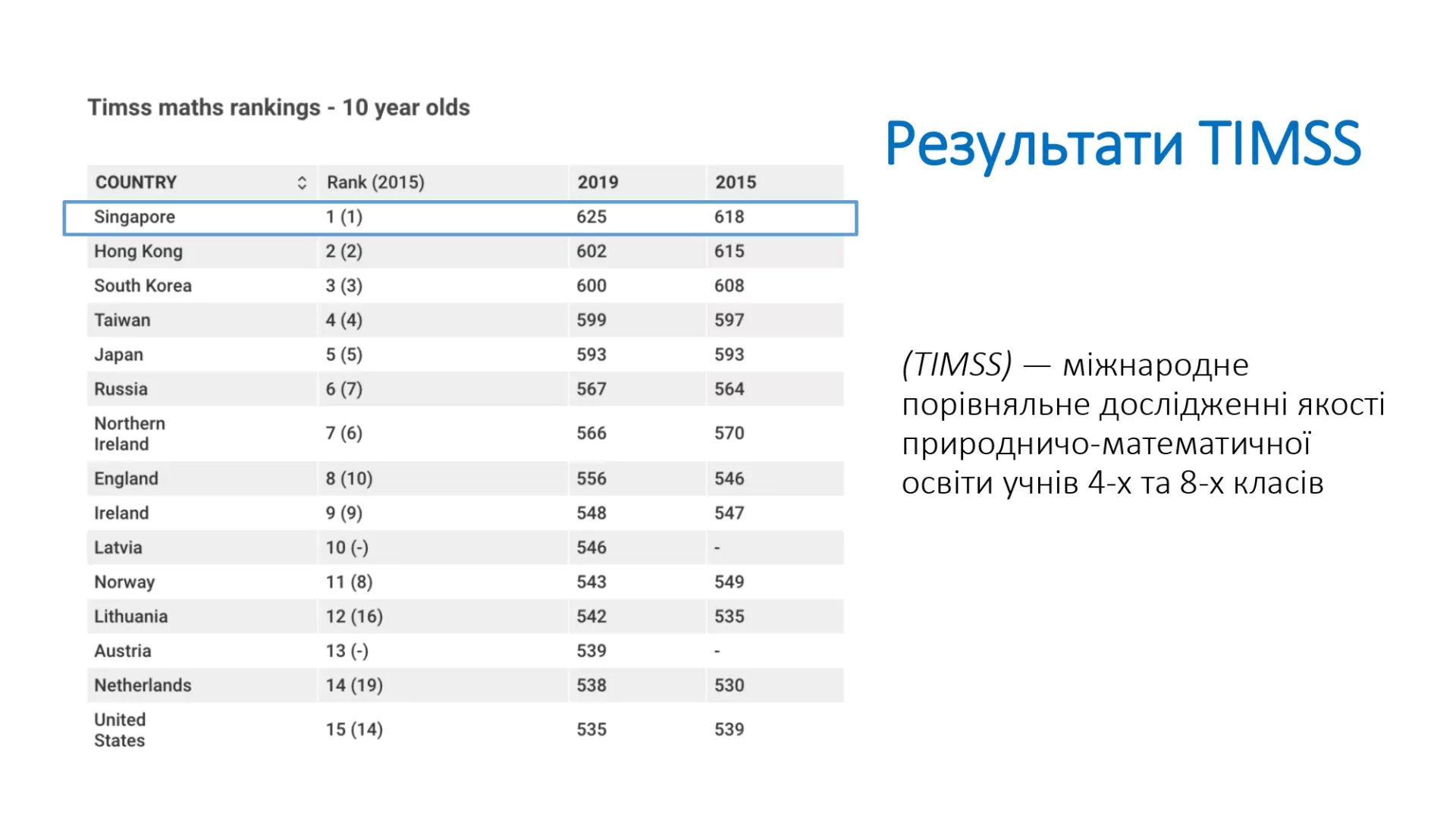
Звісно, «сінгапурська математика» — це поняття, що народилося в пресі. Адже в цій країні немає якихось окремих арифметики, алгебри, геометрії. Закони математики скрізь однакові. А ось методика викладання в Сінгапурі, дійсно, оригінальна та широко відома. З 1995 року сінгапурські школярі ставали переможцями різноманітних математичних конкурсів і демонстрували високі результати на міжнародних моніторингах. Так, у міжнародному дослідженні PISA країна регулярно посідає перші-другі місця. Міжнародне порівняльне дослідження якості природничо-математичної освіти TIMSS досліджує результати учнів 4-х та 8-х класів. Сінгапур і тут систематично забирає перші місця. 

Трохи інша ситуація з міжнародними математичними олімпіадами, на яких ця країна не має стабільних успіхів. У 2023 році Сінгапур посів 12-те місце, у 2019 не потрапив до ТОП-20 (а Україна, до слова, тоді посіла 15-те місце). Варто усвідомити, що олімпіади — це окремий рух, який не може комплексно відображати систему освіти певної країни.

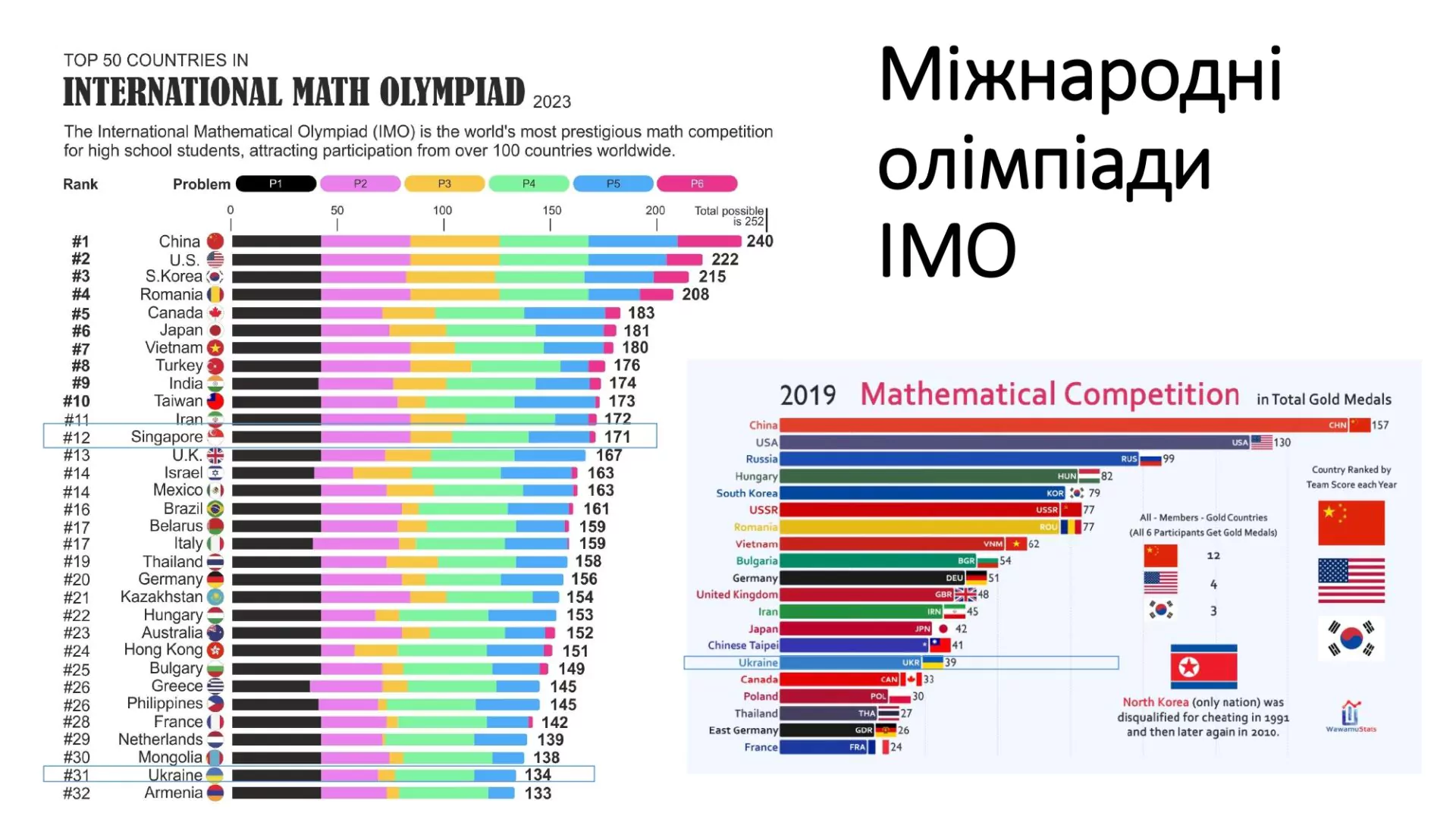
Яку гіпотезу можна висунути за цими даними? Математична освіта Сінгапуру спрямована на формування загальної картини світу, розвиток ключових компетентностей, створення бази для опанування інших предметів — тобто на міжпредметні зв’язки і застосування математичних знань для розв’язання життєвих проблем. 

Загалом увагу всього світу нині привертає країна, яка зробила ставку на освіту і швидкими темпами за 30 років перейшла з країн третього світу до країн першого. Недарма ж кажуть про сінгапурське освітнє диво. 

Звідки взялася система?

Яку ж реформу вони здійснили в освіті? Національний інститут освіти Сінгапуру проаналізував усі чинні на той час системи освіти, взяв ті елементи, які довели ефективність, і створив свій продукт на їхній основі. Тривалий час систему перевіряли, моніторили, пілотували, вкладаючи в це великі фінанси.

Що стало результатом? Чітко структурована система, яка описана в методичних рекомендаціях для вчителів. Ця система відбивається в посібниках і робочих зошитах для учнів. Проте педагогам не залишили місця для творчості під час уроку. Оскільки країна збиралася швидко досягти успіху, вона не могла бути впевнена в кожному вчителеві. Тож роль педагога дещо нівельована. Він має діяти чітко за інструкцією і не може запропонувати додаткові вправи, змінити порядок тем. Детальні методичні рекомендації по 400 сторінок регламентують геть усе: із чого розпочати урок, яка буде руханка, як підійти до викладання того чи того матеріалу, що вчитель має сказати під час виконання вправи.

Учні ж отримують великі кольорові посібники формату А4 по 100–200 сторінок і робочі зошити такого ж обсягу. Окремо такий набір є для кожного семестру. Там дуже мало теорії, натомість багато дидактичних ігор, завдань із логічним навантаженням, практичних вправ. У робочих зошитах акцент на самостійній роботі: є завдання з кожної теми, наприкінці розділу містяться підсумки — такі собі перевірчі роботи. Електронні додатки також дають змогу учням закріплювати в цікавій формі той матеріал, який вивчався, і дослідницька діяльність проводиться не лише з реальними предметами, а й з віртуальними.

У цій країні вважають, що кожен учень може засвоїти математику. У нашому суспільстві батьки й учителі можуть сказати: ця дитина — гуманітарій, їй не опанувати точні науки (хоча сучасні наукові дослідження давно спростували таку ідею), вони їй не знадобляться або вона через ментальні проблеми не зможе стрибнути вище голови. А ось у Сінгапурі переконані: матеріал на середньому рівні засвоїть кожен. Просто кожен у свій час.

У сінгапурській методиці теми тісно пов’язані одна з одною. І якщо наприкінці вивчення навчальної теми не всі учні можуть досягти бажаного результату, це не означає, що вони не опанують матеріал через певний час. На заняттях постійно повторюють попередні теми. Наприклад, у першому класі вивчають числа в межах ста, у другому — у межах тисячі, у третьому — у межах десяти тисяч, у четвертому — у межах ста тисяч, а в п’ятому — у межах мільйона. Начебто все як у нас. Але суть у тому, що на кожному із цих рівнів працюють над усім: усіма арифметичними діями (додавання, віднімання, множення, ділення), рівностями, нерівностями, рівняннями тощо. Якщо в Україні на рік вводять 4–6 тем, то в Сінгапурі їх 16–20, але не блоком, а частинками.

Увагу акцентують не на вивченні обсягів інформації, а на розумінні базових математичних концептів. Про що це? Українські вчителі звикли, що учні мають знати певні поняття, правила, що вони вміють доводити теореми. У Сінгапурі на теоретичний матеріал відводять мінімум часу. Тобто означення, якщо і подається, то дуже компактно, воно не завжди наукове, може бути побутове, описове. І завжди наприкінці опанування теми, а не одразу. Учні мають розуміти, що приховано за абстракціями, значками, словами, які реальні дії та матеріальні об’єкти із цим співвідносяться. Якщо вивчають параболу, то діти на уроці кидають м’яча. Якщо йдеться про графік — вимірюють температуру та застосовують ці дані. Якщо ж ідеться про кількість спільних точок двох кіл, то учні працюють з двома обручами.

В Україні заведено, що таблицю множення школярі вивчають. У НУШ є зрушення: її вимагають не одразу знати, а опановувати по частинках, у процесі розв’язування задач. У Сінгапурі цей підхід ще більш розтягнутий. Діти спершу дуже довго виводять множення на основі додавання, лічби парами і трійками, роботи з фішками, доміно, гральними кубиками. Ніхто не підганяє: допускається багато уроків поспіль виводити таким довгим шляхом множення, але ті, кому це набридає, у процесі такої діяльності запам’ятовують відповіді. Тож у школах дають достатньо часу, щоб кожен учень міг перейти від моделей до множення в умі. Для тих, хто йде швидше, пропонують більшу кількість завдань, і вони є складнішими.

Перший етап роботи з кожною темою: робота з реальними предметами. Другий: опрацювання малюнків. Третій: робота з абстракціями. 

Скажімо, вивчають діаграми. Спершу учні працюють зі стрічками. Наприклад, кожен учень бере у вчителя на столі стрічки одного з трьох кольорів. Дитина обирає те, що їй до вподоби. А потім у групі роздивляються, стрічок якого кольору вийшло найбільше. 

Надалі учні працюють з малюнками з реалістичним зображенням стрічок, які розташовані стовпчиками. 

На третьому етапі поступово переходять до абстракції. Спочатку стрічки позначатимуть кольоровими трикутниками, порівнюватимуть з попереднім малюнком. Потім пояснять, що насправді один трикутник може позначати кілька стрічок, тобто вчать наводити цей ключ. І лише після цього пропонують діаграми в типовій для нас формі. Ось таке повільне введення поняття. 

У цьому, звісно, допомагають об’ємні геометричні фігури, геоборди, конструктори, терези. Учні не малюють трикутники, а складають з паличок за заданими параметрами. Якщо йдуть елементи фінансової грамотності, учні оперують реальними або іграшковими грошима. Хтось удає із себе продавця, а хтось — покупця. На такі практичні вміння виділяють чимало часу. 

Починаючи з першого класу школярі відпрацьовують алгоритм: змоделювати ситуацію спершу реальними предметами, наприклад, кубиками, потім створити модель, а потім з її допомогою розв’язати задачу.

Також привчають створювати власні моделі, теж поступово. Спочатку працюють з готовими моделями, потім пропонують доповнювати наявні моделі, потім скласти задачі самостійно. Окремо оцінюється створення моделі, окремо — розв’язування задачі.

Пропонують практичні завдання: учні мають вирізати фігури та утворити з них інші або перегинанням показувати певне поняття. Наприклад, досліджують, що дійсно бісектриса ділить кут на дві рівні частини. Залучають до дослідницької діяльності.

Учні мають працювати в парах і групах, особливо під час введення нових понять. Вони обговорюють матеріал, допомагають один одному із задачами, висувають ідеї, гіпотези та навчаються обґрунтовувати. Наприклад, така дидактична гра: один з учнів витягає з коробки геометричну фігуру, ховає за спину, має описати її, назвати ознаки. Другий учень має вгадати. Потім вони міняються ролями.

У сінгапурських школах у рамках математики є окремі уроки, присвячені розвитку логічного мислення.

У 1–2-х класах є тільки формувальне оцінювання, і зворотний зв’язок надається батькам, а не учням. Тобто діти просто показують у процесі гри свої досягнення, і вчитель реагує на це. 

Із 3–4-го класу починаються систематичні діагностичні роботи, але вчитель надає лише формувальне оцінювання.

А що в Україні?

Освітній проєкт «Я дослідник 2.0» діє в Україні вже чотири роки для учнів початкової школи. Проєкт має ексклюзивні права на адаптування сінгапурської математики до українського стандарту початкової освіти. Будь-який заклад освіти може долучитися, отримати матеріали та методичні поради. Вчителі проходять підвищення кваліфікації у літніх таборах. Батьки не мають змоги придбати окремо підручники, адже сінгапурську методику викладання математики варто впроваджувати системно.